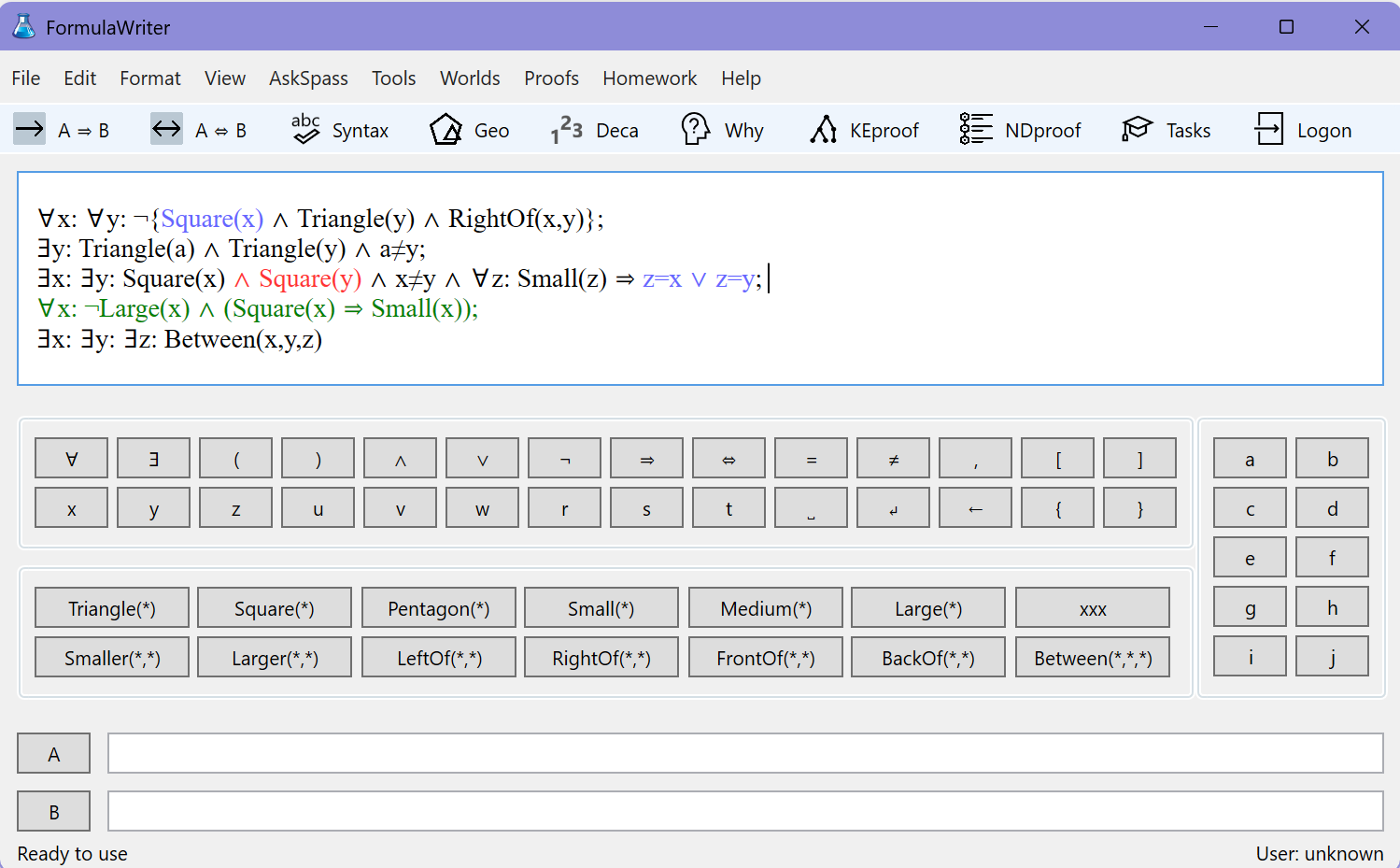
Window FormulaWriter enables you to write logical formulas very fast by clicking on buttons, and to find any syntax errors. Using menu item 'View > Buttons' you can choose between the default buttons, alternative buttons, and custum buttons. The alternative buttons are shown on the next screenshot. The custum buttons can be edited.

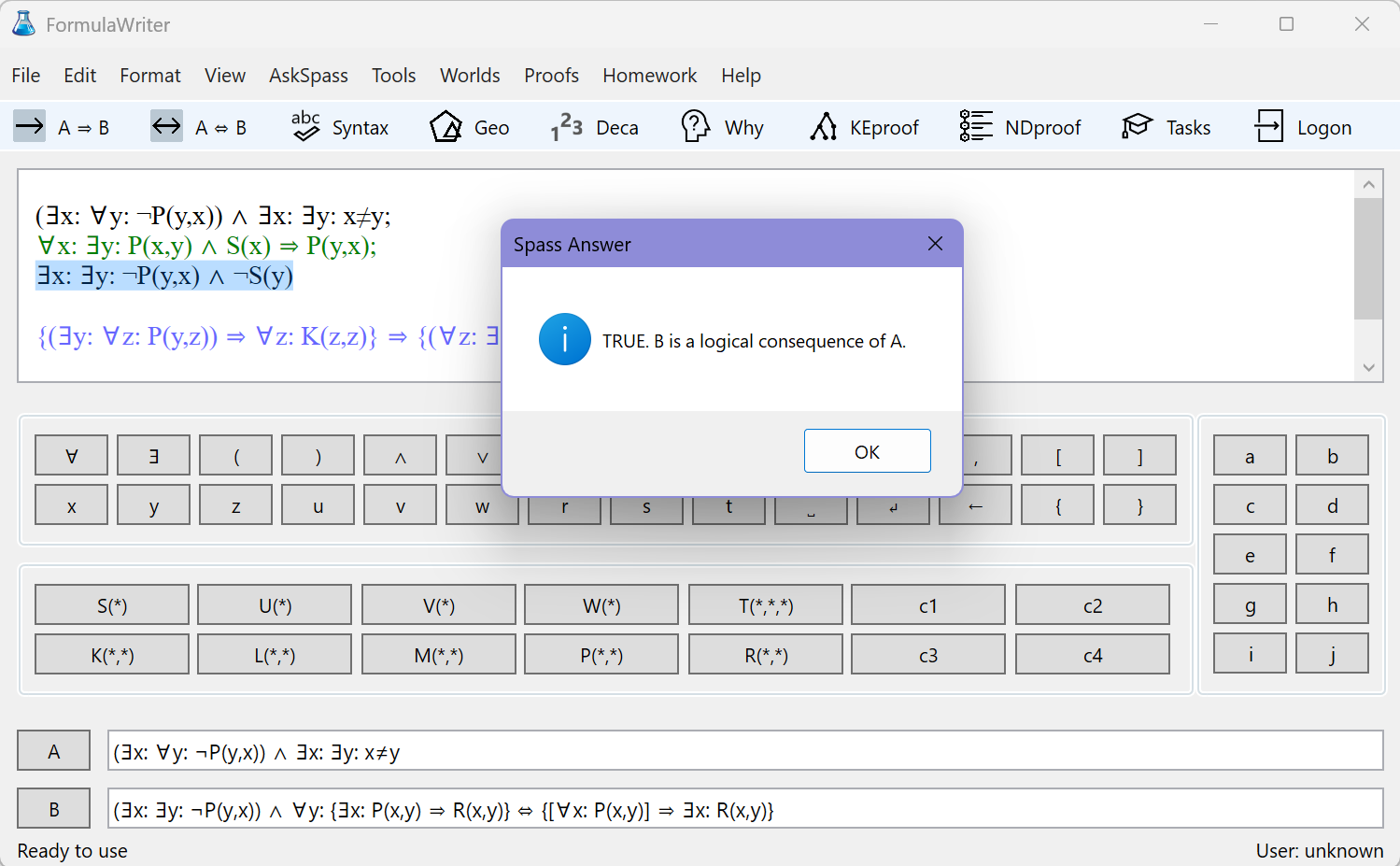
Use menu item 'AskSpass' of Window FormulaWriter to ask whether two formulas are logically equivalent, or whether a formula is a logical consequence of given hypotheses. The formulas have to be written in the text fields A and B. Separate the hypotheses with semicolons. You can manually stop the algorithm at any time. See the tooltips.

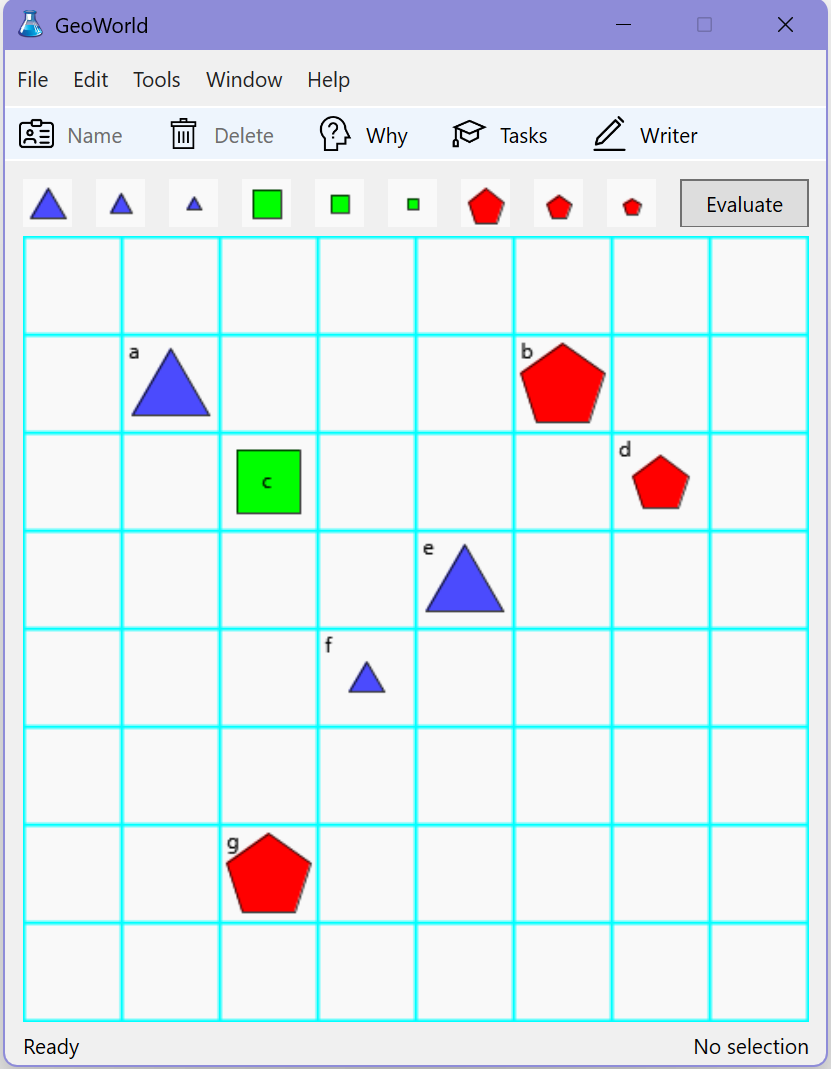
Window GeoWorld enables you to graphically construct a GeoWorld which consists of figures on a chessboard. The figures can be triangles, squares or pentagons, and can be Large, Small or Medium. Click on button 'Evaluate' to determine whether the selected logical formulas in window FormulaWriter are true or false in your GeoWorld. The formulas must be separated with semicolons, and can contain the relations displayed on the buttons in Screenshot 1. Use menu item 'Tools > Generate World' to generate a GeoWorld satisfying the selected formulas (no constants allowed in the formulas). Some homework exercises ask you to construct a GeoWorld in which given logical formulas (with constants) are true. Other exercises ask you to translate a statement about GeoWorlds, expressed in natural language, to a logical formula.

Window DecaWorld enables you to enter the description of a DecaWorld into your computer very fast. A DecaWorld is a structure with less than ten elements and any number of unary relations, binary relations, and constants. The elements are decimal digits. Click on toolbar button 'Evaluate' to determine whether the selected logical formulas in window FormulaWriter are true or false in your DecaWorld. The formulas must be separated with semicolons. Some homeworks ask the student to consruct a DecaWorld in which given formulas are true.

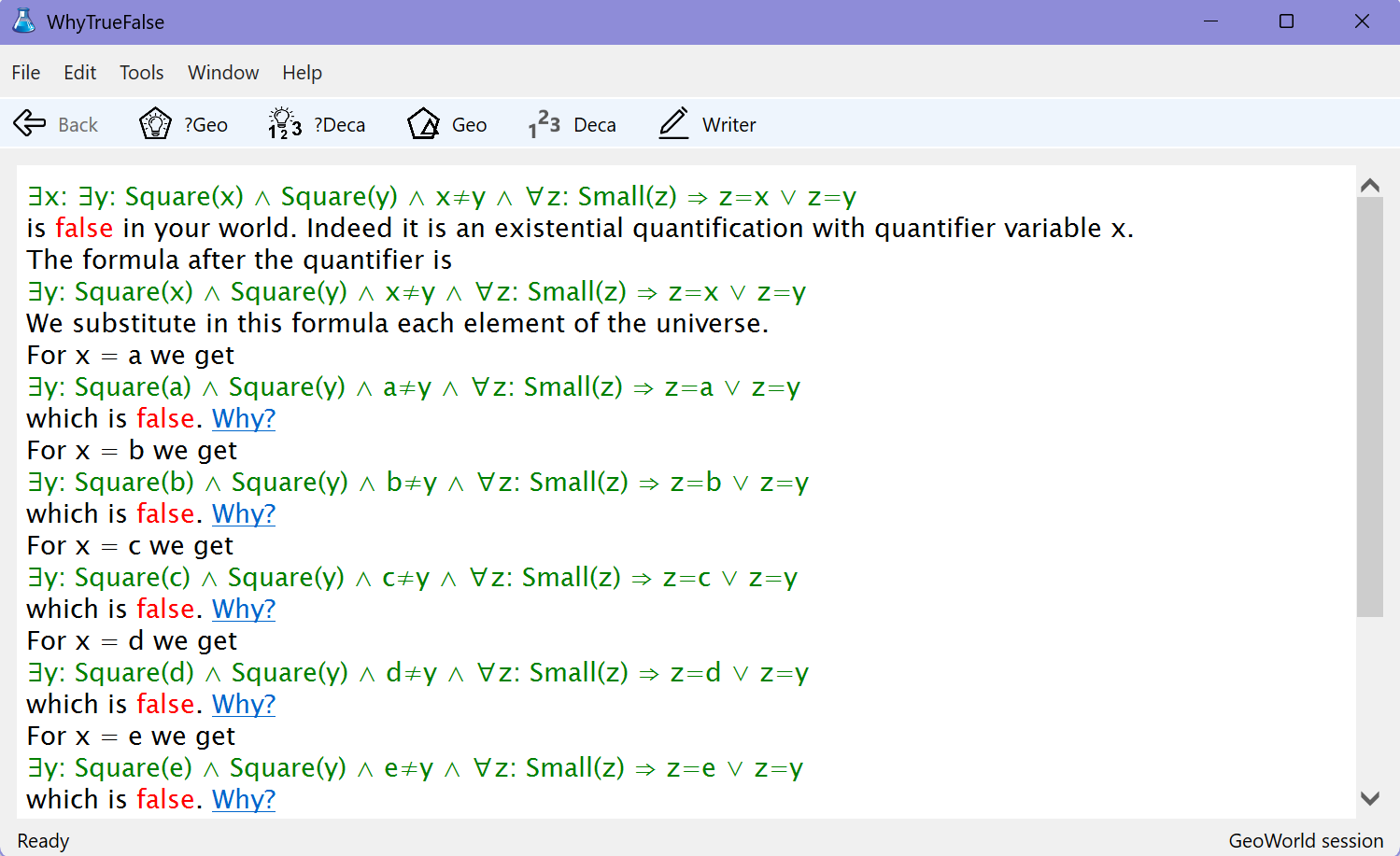
Window WhyTrueFalse enables students to obtain an explanation of why a logical formula is true (or false) in the connstructed GeoWorld or DecaWorld. To do this, students select the formula in window FormulaWriter, and click on the toolbar button '?Geo' or '?Deca' in window WhyTrueFalse. Clicking on the 'Why?' hyperlinks will provide further explanation.

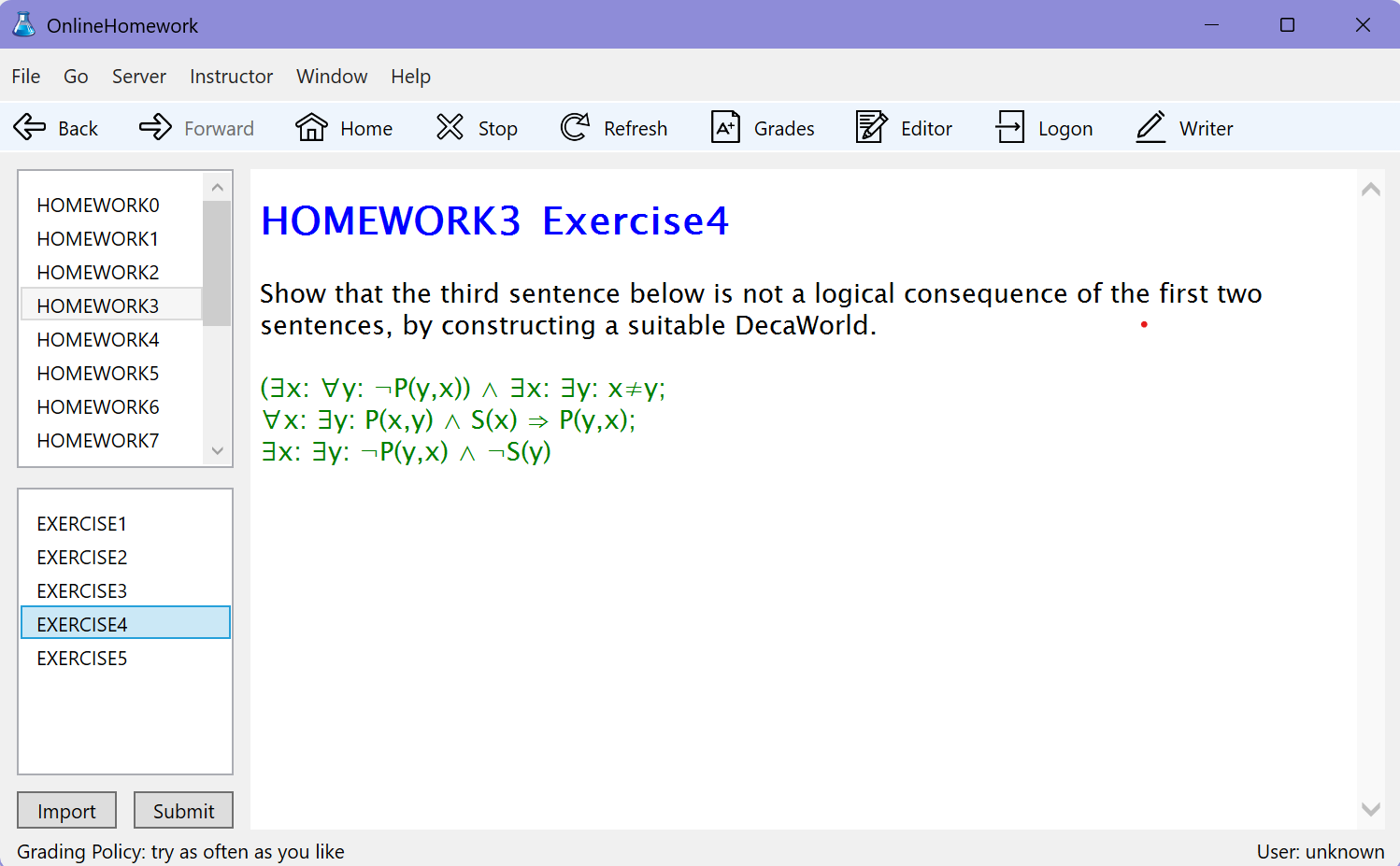
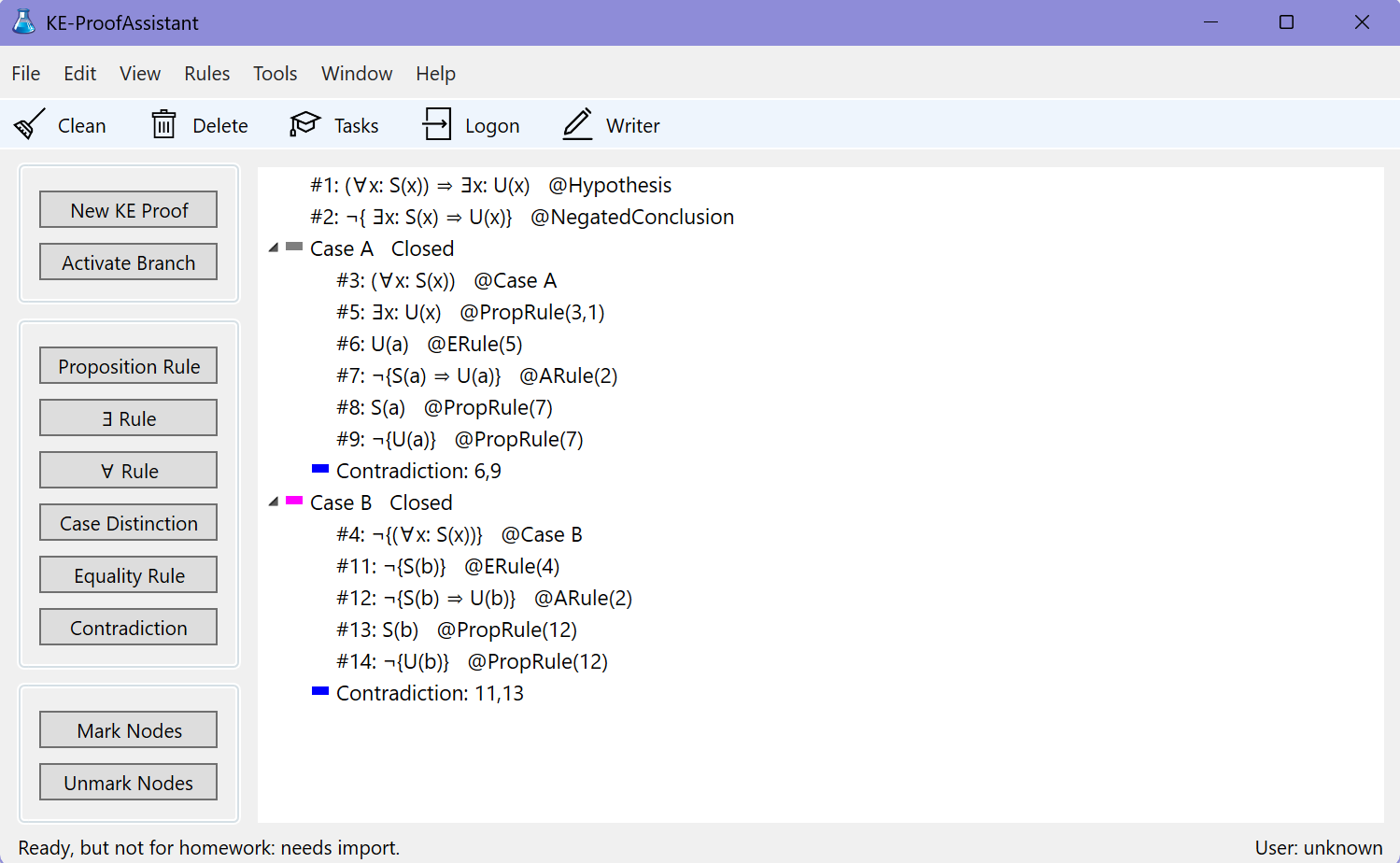
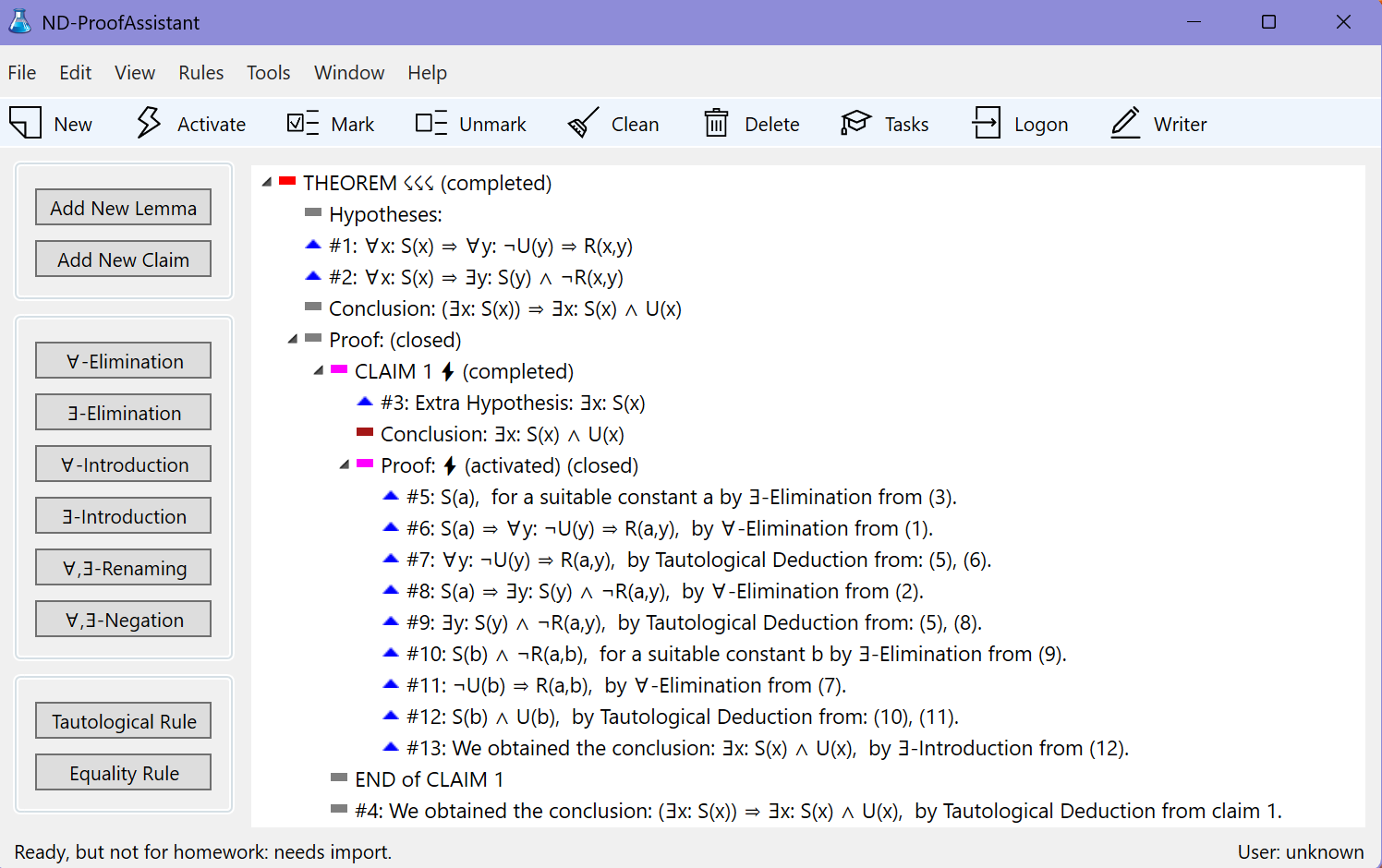
The homework exercises are displayed in window OnlineHomework. For exercises on translations or prenex normal form, the solution is a formula that must be written and selected in window FormulaWriter. Exercises that ask to make a GeoWorld or DecaWorld must be be done by constructing a suitable world in window GeoWorld or DecaWorld. Exercises on formal proofs must be imported in window KE-ProofAssistant (screenshot 7) or window ND-ProofAssistant (screenshot 8) by clicking on button 'Import' in window OnlineHomework. After an exercise is done it can be submitted to the server by clicking on button 'Submit' in window OnlineHomework. Grading will then be done automatically. All your grades are displayed by clicking the "Grades" button in the toolbar. See the tooltips.

Window KE-ProofAssistant enables students to construct correct formal proofs (in the context of predicate logic) based on Kleene Elimination. KE-proofs start by assuming the negation of what has to be proved. So it suffices to derive a contradiction. Case distinctions are allowed, and there are simple rules to eliminate quantifiers and propositional connectives, in order to deduce simpler formulas until a contradiction is obtained in each case distinction. These rules are much simpler than the deduction rules used in most other existing proof assistants. However the constructed proofs are not similar to proofs in math courses other than logic. Click here for the precise specifications.

Window ND-ProofAssistant enables students to construct correct formal proofs of theorems (in the context of predicate logic) based on a new variant of Natural Deduction. The new ND-proofs use rules to eliminate or introduce quantifiers, and rules to rename or negate quantifiers. Moreover it is allowed to use any tautological consequence of already deduced formulas, and it is permissible to use lemmas and claims that are proved separately. Unlike lemmas, claims appear within a proof. A claim inherits the hypotheses of the theorem, lemma, or claims that enclose it. The proof of a claim can use other claims that are stated within its proof, and so on. In contrast with most other proof assistants, the constructed proofs are very similar to proofs in math courses other than logic. Click here for the precise specifications.